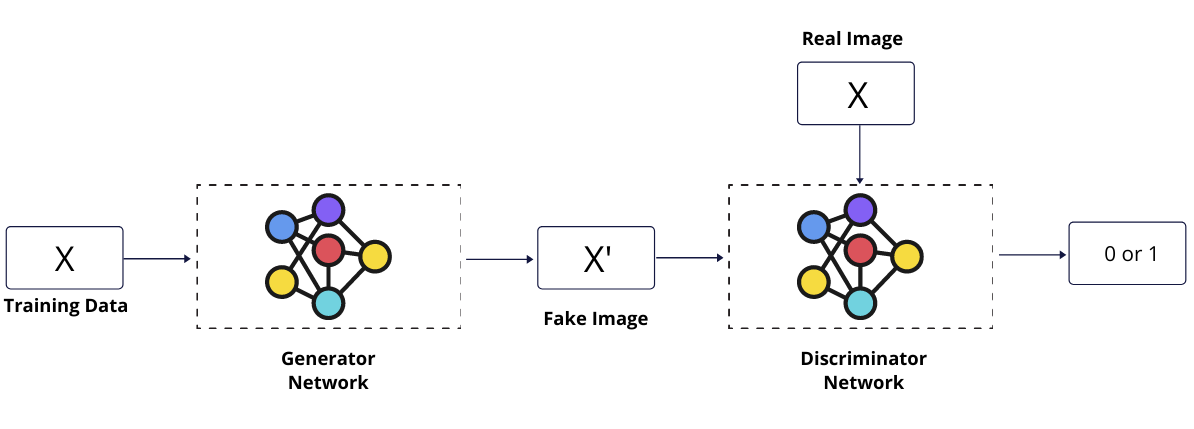
Generative Adversarial Network a.k.a GANs is a generative model which is used to generate new samples using training data. The output samples are similar to the training data but not exactly the same as our goal is to generate more diverse data from what we already have.
Goal of GANs
The distribution of generated samples should be similar to the distribution of training data without knowing what kind of distribution is this. Interesting?
If P_{data}(x) is a distribution of training data X = \{x_1, x_2, x_3 .... x_n\} and P_{model}(x) is a distribution of generated images \tilde{X} = \{x_1, x_2, x_3 .... x_n\} using a trained GAN model then the goal of generative adversarial network model is :
P_{data}(x) \approx P_{model}(x)The key idea is to introduce a latent variable that is passed through to a GENERATOR, a neural network, and generate new samples. If the distribution of generated samples is different from the distribution of original data then update the training parameter of GENERATOR and continue this process until we achieve our goal.
The question is how to ensure that Pmodel(x) is similar to Pdata(x) because we don’t calculate a likelihood value for each generated sample or training sample?
We introduce a DISCRIMINATOR, a neural network, which is a binary classifier that identifies if an image is fake or real.
if D denotes to a Discriminator, then
D(x) = \begin{cases} 1 &\text{if } x\ real \\ 0 &\text{if } x\ fake \end{cases}So Generative Adversarial Network consists of a GENERATOR and a DISCRIMINATOR. The task of the generator is to create sample data and the discriminator is to identify if a data is fake or real. So the aim of the generator is to fool the discriminator so the discriminator fails to distinguish between a fake or real sample.
GANs Training Objectives
We can formulate training objective of GANs as below
min_G max_D (E_{x \thicksim P_{data}}[\log(D(x))] + E_{x \thicksim P_{model}}[\log(1-D(G(x)))])Generator (G) tries to minimize the training objective and Discriminator (D) aims to maximize it so this is a min-max optimization problem. There are two objectives in the above expression. Let’s understand each objective and the role of the generator and the discriminator in the optimization of each part.
Objective 1:
max_D (E_{x \thicksim P_{data}}[\log(D(x))])Objective 2:
min_G E_{x \thicksim P_{model}}[\log(1-D(G(x)))])Maximization over Discriminator
The first objective of the above expression states that the Discriminator aims to maximize the likelihood value of sample x if it belongs to real sample data. And the second objective states that the Discriminator aims to D(G(x)) to 0 if x belongs to fake sample data hence maximize the second part. The generator has nothing to contribute to objective 1.
Minimization over Generator
As we mentioned, The generator aims to fool the discriminator hence it tries to make D(G(x)) = 1 so the generator tries to make objective 2 to a minimum state.
To train such networks, We use the alternative approach such that the first few iterations, we train the Discriminator and then we switch to the Generator. As this discriminator is a binary classifier, the output layer should use the Sigmoid activation function.
Optimality of GANs
The minimum Error Loss is used as the optimal condition for a supervised learning algorithm and the training goal is to achieve the least error loss. But for a Generative Adversarial Network, There are two networks to be optimized together.
For an optimal discriminator:
DS_{optimal} = P_{data}(x) / (P_{data}(x) + P_{model}(x))For an optimal generator:
G_{optimal} = P_{data}(x) = P_{model}(x)By using both together:
DS_{optimal} = P_{data}(x) / (P_{data}(x) + P_{data}(x)) = 1/2So we can conclude that at the optimal condition, the discriminator should give the .5 output value for any sample provided to it which means that the discriminator is not able to identify if an image is real or fake. As we mentioned above, the goal of the generator is to fool the discriminator, and hence, at optimal condition, our goal is achieved.
Evaluate GANs
There are two good characteristics of a good GAN model.
Recognizable Objects
The generators should generate images in which objects are clearly recognizable and any classification model can classify these objects with high confidence score.
Semantically Diverse
The generators should generate images of all classes which exist in the training data. If an generator generates images of a particular class label, then it is not well generalized model.
There are two popular metrics which is used to evaluate GANs are Inception Score and Frenchte Inception Distance.
Inception Score (IS)
Inception Score has two quantities which can be correlated with Recognizable Objects and Semantically Diverse characteristics of a GAN model.
IS = exp(H(y) - H(y|x))H(y) denotes the entropy of generated class labels by the generator. A high entropy value means generated data is equally distributed among the different classes. It satisfies the Semantically diverse characteristic.
H(y|x) denotes the entropy of the class label predicted by the classifier for different data. A low entropy value means a particular class label has a high confidence score so the object is easily recognizable in the generated image.
So, A high value of Inception Score is better for a generative model.
One drawback of the Inception Score is that it doesn’t consider training data in its metrics so that is purely based on generated samples. Though the goal of a GANs model is to generate data which distribution is close to real data distribution.
Frechet Inception Distance (FID)
This method considers both training and generated samples for its calculation and our goal is to have minimum distance between training and generated samples.
This method calculate the distance between the two distributions:
d^2((M_{model},COV_{model}),(M_{data},COV_{data})) = (\|M_{model} - M_{data}\|_2^2) - Trac(COV_{model} + COV_{data} - 2 * (COV_{model}.COV_{data})^2)M denotes mean and COV covariance.
Here we’re calculating the distance between generated samples distribution and real data distribution.
The low value of Frechet Inception Distance is better for a generative model. Low Value tells that generated samples are close to the real samples.