How Does Variational Autoencoder Work? Explained!

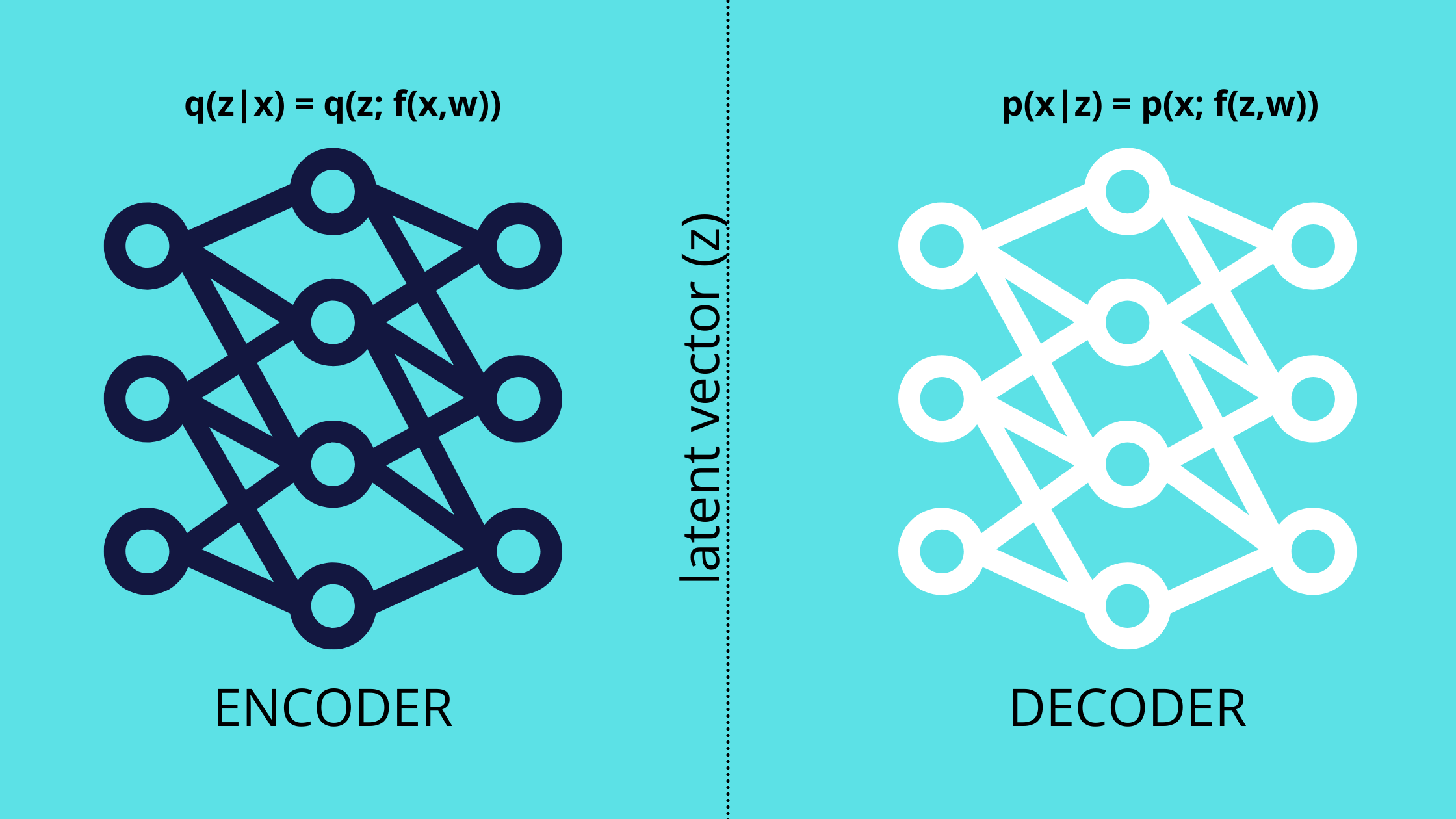
Variational Autoencoder is a an explicit type generative model which is used to generate new sample data using past data. VAEs do a mapping between latent variables, dominate to explain the training data and underlying distribution of the training data. These latent variables vectors can be used to reconstruct the new sample data which is close to the real data.

VAEs consists of two types of neural network in their architecture: Encoder and Decoder. The encoder outputs the mean and covariance corresponds to the posterior probability of given training data and the decoder takes latent vector sampled from the output of the encoder and reconstructs the sample data.

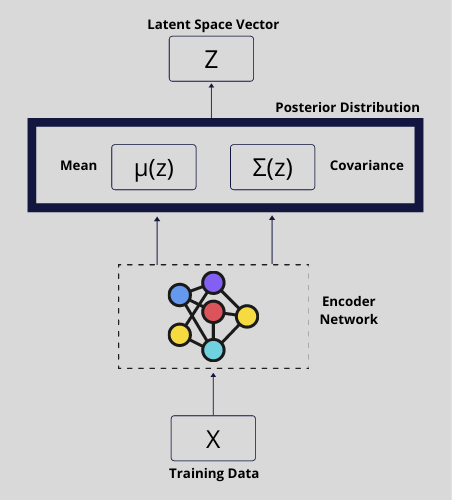
ENCODER in VAEs

It takes training data as input and output the mean \mu^z and covariance \Sigma^z corresponds to approximate posterior distribution of P_\varPhi(z|x) . From which, a sample latent vector z is taken and pass through to the decoder.

The objective of the encoder is to apply a constraint on the network such that posterior distribution P_\varPhi(z|x) is close to the prior unit gaussian distribution P_\Theta(z)

This way regularization is applied on the network and the objective is to maximize the negative of KL divergence distance between P_\varPhi(z|x) and \approx P_\Theta(z)

Next, Instead of passing the whole output of the encoder to the next bottleneck layer, we take a sample (z) using the reparameterization method. This reparametrization method helps gradients to backpropagate from decoder to encoder through this bottleneck layer.

z = \mu(z) + \Sigma(z) * \epsilon where \epsilon = \Nu(0,1)

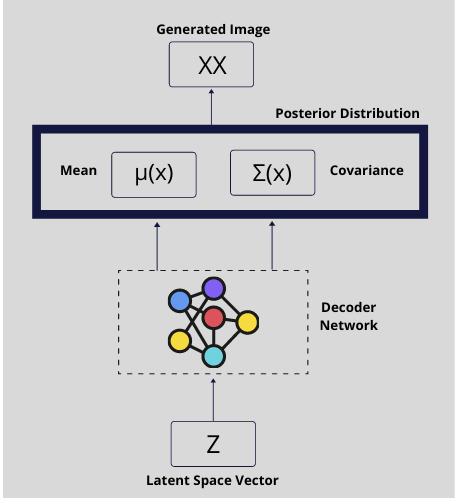
DECODER in VAEs

It takes latent space vector z, sampled out from the encoder using reparameterization method, as input and output the mean \mu^x and covariance \Sigma^x corresponds to posterior distribution of P_\Theta(x|z) . From which, a new sample can be generated.

The objective of the decoder to regenerate the sample data which is close to the original data.

Here log(p_\Theta(x|z)) is the reconstruction loss so this should be close to the original data distribution. To maximize this loglikelihood, we can use the mean squared error.

Combining Encoder and Decoder

So the overall objective of a variational autoencoder model is given as below:

Here \varPhi is the parameter of the encoder network and \Theta is the parameter of the decoder network. The goal of training is to learn these parameters.

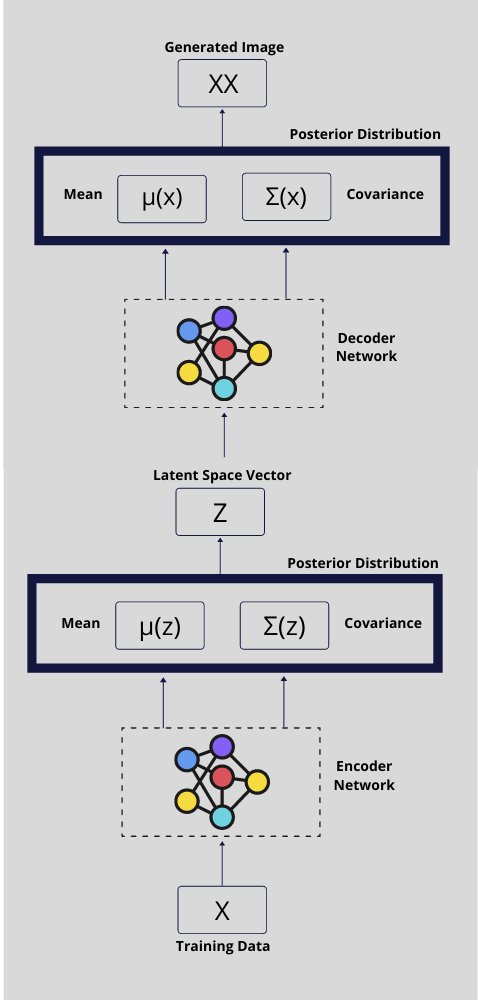
Once a VAEs model trained, The encoder part can be discarded and decoder part is used to generated new sample data by passing a Gaussian latent vector (Z).