What is the difference between Variance and Bias in Machine Learning?

From the perspective of Supervised Machine Learning, we know all models have errors. We need to minimize the error so as to make the model useful. For this, we need to minimize two major sources of error- Bias and Variance.

What is Bias?

The tendency of the algorithm to learn wrong details from the dataset by not taking into consideration all the information. It is the difference between the predicted value and the correct value which we need to predict.

High bias means inaccurate predictions. Parametric algorithms are prone to high bias. Parametric model summarizes data with a set of parameters of fixed size. Since these models pay very little attention to the training data and too much simplifies it. Therefore, leads to a high error on training and testing data(hence underfitting it). For example Linear Regression, Linear Discriminant Analysis, and Logistic Regression.

What is a Variance?

A variance occurs when the models work too good on training data. But does not work well on testing data or validation data. It shows how much scattered is the predicted value from the actual value. High variance causes the algorithm to model the random things in the training data. Instead of the intended output(hence overfitting it).

Bias and variance using the bulls-eye diagram

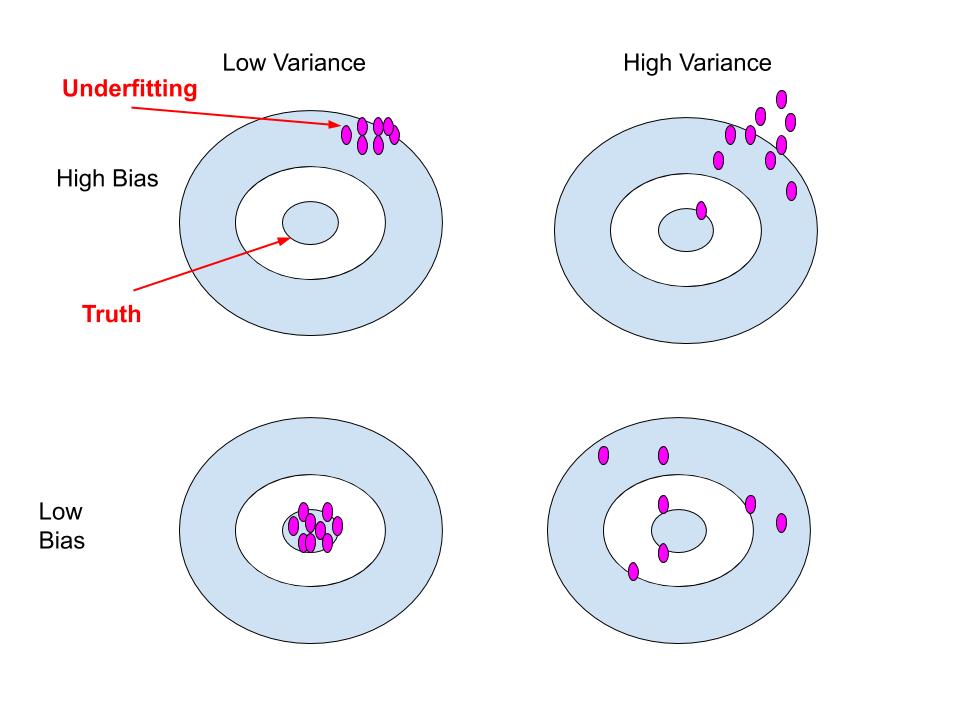
From the diagram, we can say that the centre of the target is a model that perfectly predicts correct values. As we move away from the bulls-eye our predictions become get moreover worse.

In Supervised learning, we mostly face problems of underfitting and overfitting. When the model is unable to determine the underlying pattern of the data we face the underfitting problem. This problem arises when the dataset is small or when we try to build a linear model with a non-linear model. When the model captures noise along with the underlying pattern in data we face overfitting problem. These models have low bias and high variance, similar to Decision Trees which are prone to overfitting.

High Bias Low Variance: Consistent models but inaccurate on average.

High Bias High Variance: Inaccurate models and also inconsistent on average

Low Bias Low Variance: Accurate models and consistent on averages. We want this in our model.

Low Bias High variance: Somewhat accurate models but inconsistent on averages.